Yuhai Tuの論文を読み解く-04

・式 [4]の下，p.14856，左段落，上から六行目

ここには，

\( \Large \displaystyle C \equiv \frac{K_I}{K_A} < 1\)

\( \Large \displaystyle L \rightarrow \infty, \hspace{ 20pt } f_L(L) \rightarrow -ln \ C \)

とさりげなく書かれています，これを導き出しましょう．

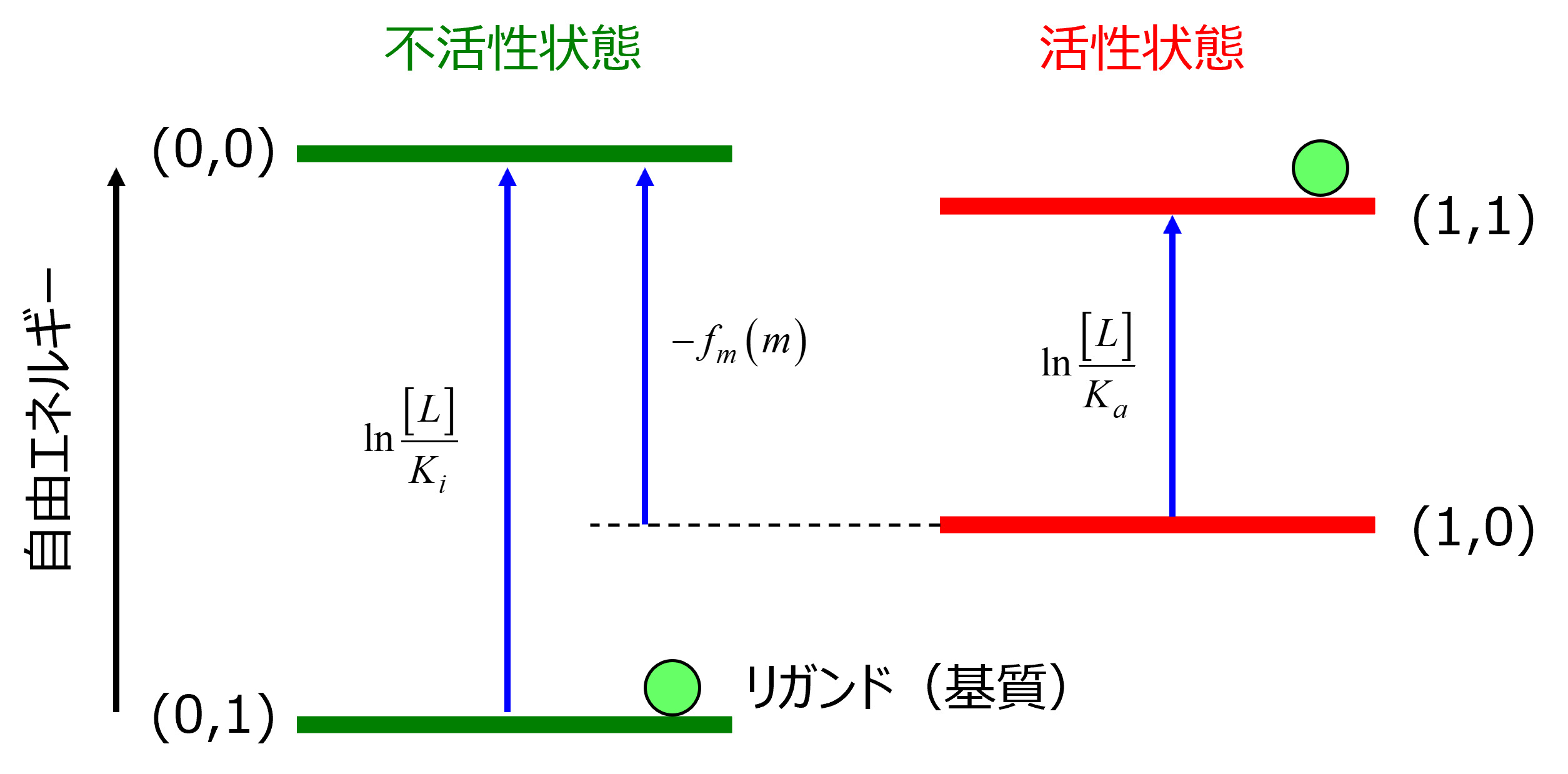
エネルギー状態は，

ここでは，
　P（0，0）　：　不活性，　リガンド未結合
　P（0，1）　：　不活性，　リガンド結合
　P（0，0）　：　活性，　　リガンド未結合
　P（0，0）　：　活性，　　リガンド結合

の4状態を考えます．

・Cの定義

\( \Large \displaystyle \frac{P(0,1)}{P(0,1)} = \frac{L}{K_i} \rightarrow \Delta E_i = ln \frac{L}{K_i} \)

\( \Large \displaystyle \frac{P(1,1)}{P(1,1)} = \frac{L}{K_a} \rightarrow \Delta E_a = ln \frac{L}{K_a} \)\

となるので，

\( \Large \displaystyle \frac{K_i}{K_a} = \frac{\Delta E_a}{\Delta E_i} \)

となります．上の図で設定したように，

\( \Large \displaystyle \Delta E_a < \Delta E_i \)　なので，

\( \Large \displaystyle C \equiv \frac{K_i}{K_a} < 1 \)

となります．

・リガンド濃度が無限大の場合

\( \Large \displaystyle f_L (L) = ln \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} = ln \frac{ \frac{1}{L} + \frac{1}{K_i}}{ \frac{1}{L} + \frac{1}{K_a}} \)

です（分子・分母をLで割った）

L→無限大だと，

\( \Large \displaystyle f_L ( \infty ) = ln \frac{ \frac{1}{ \infty} + \frac{1}{K_i}}{ \frac{1}{ \infty} + \frac{1}{K_a}} = ln \frac{K_a }{K_i} = - ln \ C \)

・なぜ，\( \Large \displaystyle \Delta E_a < \Delta E_i \)，なのか

なぜ，彼らがこのような状態を考えたのか，推論していきましょう．

もし，C>1，だとしたらどうなるのでしょう？

リガンドが無限大の場合，

\( \Large \displaystyle f_L ( \infty ) = - ln \ C < 0 \)

となり，マイナスの値となります．ということは，

リガンドが飽和的に結合すると，エネルギー準位が逆転する，ということになるのでしょうか？

なので，C<1，と考えているのだと思います（多分です．．．．）